Linearizações

Linearização das contagens

Tivemos uma discussão interessante com um experimentador, a oportunidade de aumentar a taxa de amostragem, usando um ADC de hardware 500 ksps um 13 pouco. A intenção deste investigador é capaz de contar pulsos, embora eles são muito próximos. Seu objetivo é chegar aos dez mil cps (em comparação com cerca de 1000 atual cps).

Na verdade não há nenhum ponto preciso além do qual não podemos mais contar, mas um aumento gradual da probabilidade de sobreposição de impulsos (Acumular-se). Fizemos alguns testes e verificamos que até 100 linearidade cps é excelente, em 500 cps começamos a experimentar um significativo número de colisões.

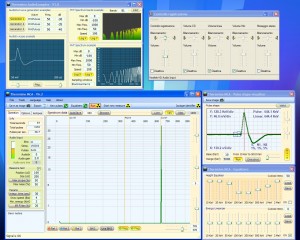
As imagens seguintes mostram os testes com pulso simulado (o simulador de impulsos produz impulsos folgado 150 uS semelhantes aos do nosso PmtAdapter)

• imagem da esquerda 1 ímpeto 50 vezes por segundo, total 50 CPS
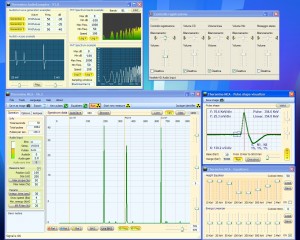
• centro da imagem 3 pulso 50 vezes por segundo, total 150 CPS
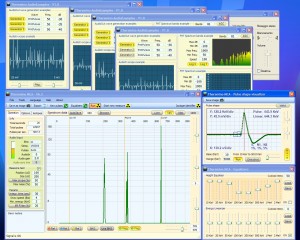
• imagem direita 10 pulso 50 vezes por segundo, total 500 CPS

Os impulsos medidos nestes três exemplos são suficientemente perto 50, 150 e 500 cps teóricas, mas pode mudar se você desligar e ligar alguns dos geradores de teste. Quando você ligar um gerador que leva um novo local aleatório no trem de pulso. Dois geradores pode contar exatamente sobreposta por um e repetir o erro todos os ciclos, mas isso não acontece com dados aleatórios a partir de um PMT.

Pode-se ir até um máximo de 1000, 5000 e mesmo até 10000 CPS, mas com uma perda progressiva gradual de impulsos (perda de linearidade na parte superior do intervalo de medição)

Em 10000 cps o número de impulsos perdidos, Seria muito alta (sobre 90% e mais além) mas poderia ser compensado, tendo em conta o aumento progressivo da probabilidade de colisão. A fórmula estatística é simples e produz uma correcção de linearidade preciso. (aqueles interessados ​​em sua implementação encontra nas fontes ThereminoGeiger – procurar todas as ocorrências: “DEADTIME”)

Linearizar a resposta com métodos estatísticos não degrada o desempenho de resolução e sensibilidade e, portanto, melhor que agir com o hardware força bruta (por exemplo, aumentar a velocidade da ADC, ou usar uma amostra-hold)

– – – – – – –

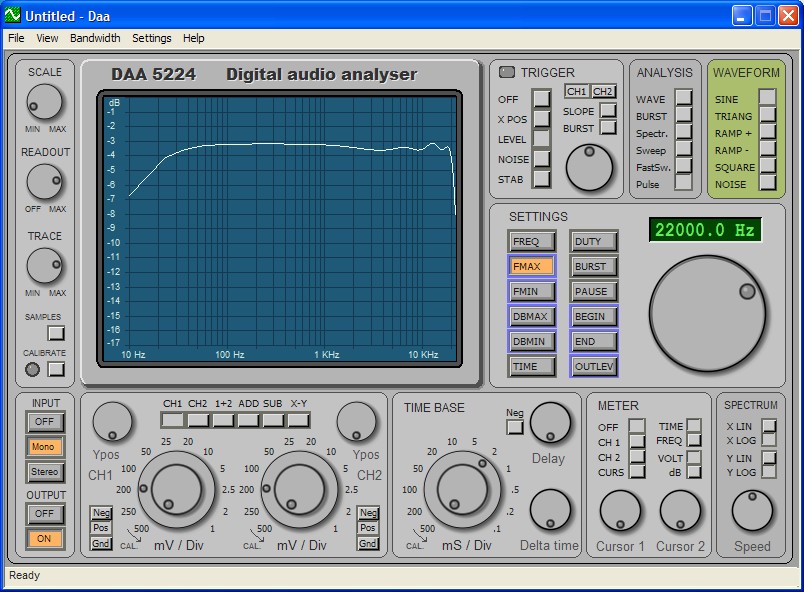
Estes teste interessante ter trazido a nossa atenção sobre a largura de banda, todas as placas de som está limitado a cerca de 22 kHz. A taxa mínima de amostra seria então 44 kHz (lei Nyquist), mas internamente as placas de implementar uma sobre-amostragem, a volte x2 (e eles são, portanto, definidos pela 96 kHz) a volte x4 (e eles são, portanto, ser 192 kHz). Em todos os casos, os dados são então interpolados 192 kHz, gerar impulsos com tendência muito gradual. E isso é exatamente o que você precisa, para medir com precisão o pico pulso.

Aqui você vê a largura de banda de placas de áudio, variando de 10 Hz a 22 kHz.

Se você usar um ADC sem largura de banda, no entanto, devemos integrar dados, até chegarem impulsos suaves, para ser capaz de medir com precisão.

sem a integração, o ruído seria muito alta, porque banda passante exagerada. Em seguida, ele perde a oportunidade, para ver os isótopos de baixa energia e também a sensibilidade e resolução, seria reduzido.

– – – – – – –

Centrar-se muito sobre a taxa de amostragem, à custa de tudo o resto, Não é uma boa idéia. idealmente, Poderia aumentar os dois maiores contagens, três, ou no máximo, dez vezes, mas na prática não seria suficiente, fazer exemplos:

As redes de detecção de terremotos têm o mesmo problema, todos os geofones perto de eventos catastróficos, saturano e seus dados são simplesmente descartados.

Se fosse para usar sensores capazes de suportar esses eventos, você deve descartá-las da mesma, por causa dos erros de medição fortes causada por descontinuidades que ocorrem perto do epicentro.

No caso de terremotos, as descontinuidades são devido a fraturas do solo e descontinuidades devido a pedras e areia localizada. Mas, no caso da explosão do centro, vêm Fukushima e Chernobyl, as descontinuidades são devido à projecção de fragmentos relativamente grandes, rasgada a partir das barras de núcleo.

Os fragmentos maiores cair em uma área de dezenas de quilómetros, tornando-se totalmente não confiável de todos que os sensores de área. Se um fragmento, tal como a encontrada em um canteiro de flores a partir de Bionerd23 (www.youtube.com/watch?v = ejZyDvtX85Y), Ela cai na vizinhança do sensor, Este irá medir valores muito elevados, respeito a toda a área circundante.

Você poderia ter erros de medição enormes (até mesmo 100 vezes), movendo-se a poucos metros. Luma mistura de isótopos Seria completamente alterada, dependendo da composição do fragmento.

– – – – – – – – –

Tomemos por exemplo a rede ambientalista alemã, com base em 1800 sensório Geiger, espaçados, em média, dez quilómetros uma da outra. No caso do evento verdadeiramente catastrófica, você deve descartar quatro ou até dez sensores, mas os restantes 1790 iria fornecer dados, que extrapolados, permitem definir a exata radioatividade epicentro.

A lei de atenuação quadrática, Ele pode fornecer resultados muito mais precisa do que eles poderiam fazer sensores descartados.

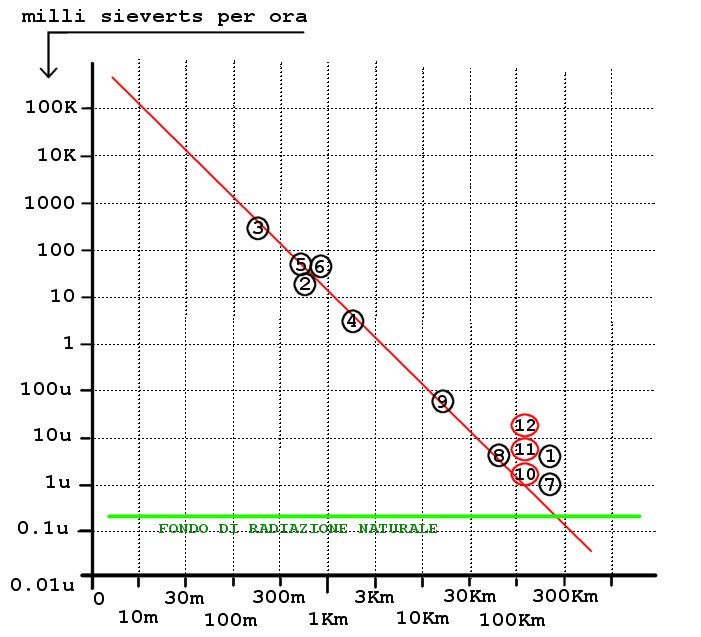
A imagem a seguir é parte de um artigo, publicado após o acidente Fukushima, e é baseado em dados publicados no 15 dias após a explosão do reactor 3.

– PDF Document: Probabilidade e riscos

– Decumento ODT para tradutores: Probabilidade e riscos

(1) 15/03/2011 a Tokyo 3 micro-Sievert / ora ( 10 vezes a radiação de fundo natural )
(2) 15/03/2011 “à entrada do centro” 11.9 mili-Sievert / hora
(3) 15/03/2011 “perto do reactor de três” 400 mili-Sievert / hora
(4) 17/03/2011 medida a partir de helicópteros 4.13 mili-Sievert de 1000 pés de altura ( 1600m )
(5) 17/03/2011 medida a partir de helicópteros 50 mili-Sievert de 400 pés de altura ( 640m )
(6) 17/03/2011 medida a partir de helicópteros 87.7 mili-Sievert de 300 pés de altura ( 480m )
(7) 18/03/2011 Tokyo medido um nível de radiação de cerca de 1 micro-Sievert / ora
(8) 18/03/2011 em 60 quilómetros a partir do centro 6,7 micro-Sievert / ora.
(9) 18/03/2011 em 20 quilómetros a partir do centro 80 micro-Sievert / ora.
(10) 18/03/2011 um Ibaraky 140 quilómetros a partir do centro 2.5 micro-Sievert / ora.
(11) 20/03/2011 um Ibaraky 140 quilómetros a partir do centro 6.7 micro-Sievert / ora.
(12) 21/03/2011 um Ibaraky 140 quilómetros a partir do centro 12 micro-Sievert / ora.

Os dados publicados pela “Ministro da Educação” (www.mext.go.jp), De “Divisão de Segurança Nuclear (www.bousai.ne.jp/eng) e Prefeitura de Fukushima, após voos de helicóptero.

Nesta imagem você pode ver três coisas:

• A lei de atenuação quadrática é plenamente respeitado. (erros mínimos no que diz respeito aos erros dos sensores)

• Os dados são extrapolados de perto para o evento.

• Você pode definir o valor de radioatividade até a poucos metros a explosão com grande precisão.

Com uma rede de milhares de estações que você poderia ter uma grande precisão, mas, a fim não descartar os dados de alguns sensores, Seria degradar a qualidade toda a rede. Pelo contrário, seria melhor para continuar na direção oposta e tentar diminuir o ruído e maximizar a sensibilidade e a separação dos isótopos.

Com sensores de Nai(TL) a resolução é baixa e há sempre a possibilidade real de medir um isótopo em vez de outro. Quanto maior for a resolução diminui, a maior este risco.

energias linearização

Theremino MCA usa um equalizador semelhante ao equalizadores gráficos para linearizar as energias e amplitudes dos gráficos.

Muitas dúvidas expressas que este método é menos preciso do que a dos pontos com energia selecionável (paramétrico Equalizador) usado, Por exemplo,, na versão 6 PRA.

Por isso, é necessário explicar as razões para esta escolha.

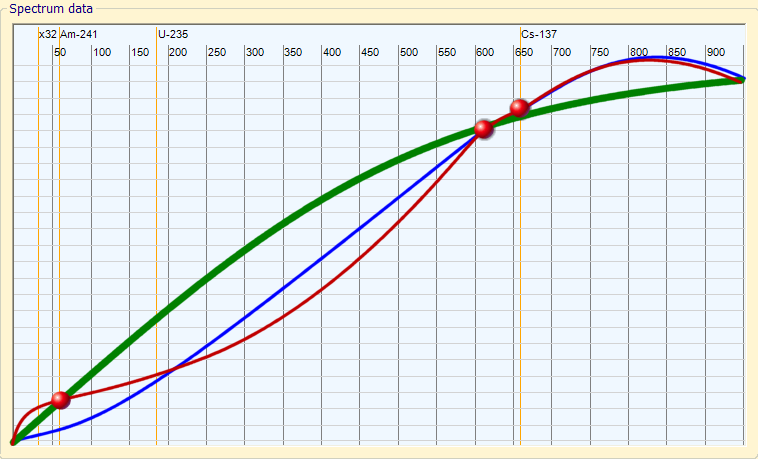
pontos arbitrários de linearização, não uniformemente distribuída ao longo do espectro, Pode produzir curvas não naturais e grandes erros.

VERDE: A melhor curva de linearização, que minimiza os erros.
BLU: A curva de linearização que é obtido através da correcção “quase” exatamente 609 e o 662 Kev
ROSSO: A última curva, depois de corrigir “exatamente” até mesmo o 59 Kev

“Língua italiana” – Grandes erros produzidos por um sistema de linearização “preciso” —————————————————————————————————————————————————————— 1) Os corrige usuário “exatamente” um pico de Cs-137 662 Kev (com uma amostra de césio)

2) Os corrige usuário “exatamente” um pico de Bi-214 para 609 Kev (com uma amostra de rádio)

3) Devido à imprecisão introduzida pela grande FWHM das linhas, e também porque o número de lixeiras não é infinito, aqueles “exato” Correções não são tão “exato”

4) Como a distância entre os dois pontos de correção (609 e 662) ele é pequeno, qualquer pequena imprecisão extrapola um grande erro em toda a curva de correção.

5) Você testar uma amostra de Am-241 59,536 Kev, Ele descobre um grande erro, e corrige “exatamente” o pico.

6) O utilizador de teste uma amostra de Co-60 1.3 MeV, Ele descobre um grande erro, e corrige “exatamente” este erro.

7) O usuário agora está muito feliz, tudo 4 As amostras são “exatamente” corrigir e sua linearidade é absolutamente perfeito …. vero?

Não! a curva “invisível” resultado é mais parecido com uma cobra do que uma curva do mundo real. somente pontos 59, 609, 662 e 1300 Kev está exatamente correto, todas as outras energias estão errados, e com mais erros do que aqueles que ocorreria sem o uso de qualquer correção. análises de todas as futuras feitas por este “usuário feliz” detectar com “precisão” isótopos que podem ser encontrados apenas em amostras do planeta Marte.

 

“língua Inglesa” – Grandes erros produzidos por um “preciso” método de linearização —————————————————————————————————————————————————————— 1) Os corrige usuário “exatamente” um pico Cs-137 em 662 Kev (usando uma amostra de césio)

2) Os corrige usuário “exatamente” um pico de Bi-214 em 609 Kev (utilizando uma amostra de rádio)

3) Devido à imprecisão introduzido pelo grande FWHM das linhas, e porque o número bin não é infinito, Essa “exato” correções não são tão “exato”

4) Como a distância entre os dois pontos de correção (609 e 662) é pequeno, cada pequena imprecisão extrapola um grande erro em toda a curva de correção.

5) O utilizador testa uma amostra Am-241 em 59.536 Kev, descobre um grande erro, e corrige “exatamente” a 59 pico KeV

6) O utilizador testa uma amostra de Co-60 no 1.3 MeV, descobre um grande erro, e corrige “exatamente” esse erro

7) O usuário agora está muito feliz, todos 4 As amostras são “exatamente” corrigidas e a linearidade é absolutamente perfeito…. é verdade ?

Não! O “invisível” curva resultante é mais parecida com uma cobra, do que uma curva mundo real. Somente os pontos em 59, 609, 662 e 1300 KeV são exatamente corrigido, todas as outras energias estão errados, e com mais erros do que antes desta “linearização” Todas as futuras análises feitas por este “usuário feliz” vai encontrar com “precisão” isótopos que podem ser encontrados apenas em amostras provenientes de Marte planeta.

overfitting

Na Wikipedia você pode ler uma boa explicação para este efeito: http://en.wikipedia.org/wiki/Overfitting

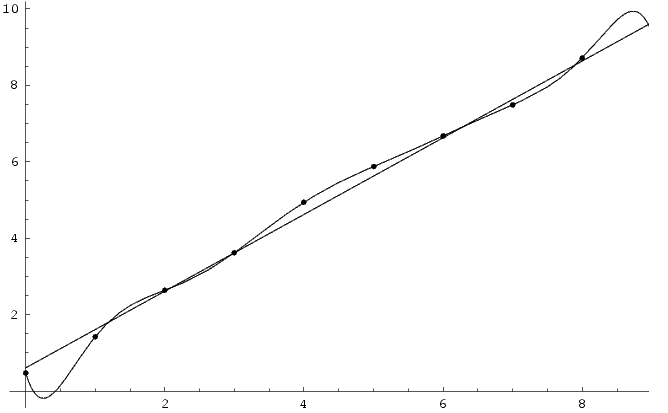
Wikipedia mostra e explica isso muito bem que:

ITALIANO: Embora a função de linearização passos exatamente para todos os pontos que se obtém um resultado melhor com uma linha reta.

Inglês: Embora a função polinomial passa através de cada ponto de dados, a versão linear é um ajuste melhor.