Linearizzazioni

Linearizzazione dei conteggi

Abbiamo avuto una interessante discussione con uno sperimentatore, sulla opportunità di incrementare la frequenza di campionamento, usando un ADC hardware da 500 ksps a 13 bit. L’intento di questo sperimentatore è poter contare gli impulsi, anche se sono molto vicini tra loro. Il suo obiettivo è di arrivare verso i diecimila cps (contro i circa 1000 cps attuali).

In effetti non esiste un punto preciso oltre il quale non si riesce più a contare, ma un graduale aumento della probabilità di sovrapposizione degli impulsi (PileUp). Abbiamo fatto alcune prove e abbiamo verificato che fino a 100 cps la linearità è ottima, a 500 cps si comincia a verificare un numero significativo di collisioni.

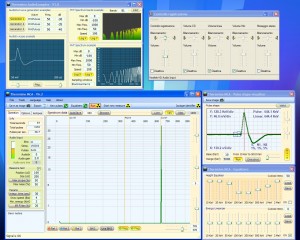
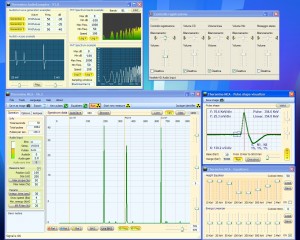
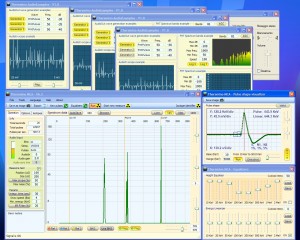
Nelle seguenti immagini si vedono i test con impulsi simulati (il simulatore di impulsi produce impulsi larghi 150 uS simili a quelli del nostro PmtAdapter)

      

• Immagine di sinistra 1 impulso 50 volte al secondo, totale 50 CPS
• Immagine centrale 3 impulsi 50 volte al secondo, totale 150 CPS
• Immagine di destra 10 impulsi 50 volte al secondo, totale 500 CPS

Gli impulsi misurati in questi tre esempi sono abbastanza vicini ai 50, 150 e 500 cps teorici ma possono cambiare se si spengono e accendono alcuni dei generatori di test. Quando si accende un generatore questo prende una nuova collocazione casuale nel treno di impulsi. Due generatori esattamente sovrapposti possono contare per uno e ripetere l’errore tutti i cicli, ma questo non succederebbe con i dati casuali provenienti da un PMT.

Si potrebbe proseguire anche fino a 1000, 5000 e anche fino a 10000 cps, ma con una progressiva graduale perdita di impulsi (perdita di linearità nella parte alta del campo di misurazione)

A 10000 cps il numero di impulsi persi, sarebbe molto alto (circa il 90% e oltre) ma potrebbe essere compensato, tenendo conto del progressivo aumento di probabilità di collisione. La formula statistica è semplice e produce una precisa correzione della linearità. (chi è interessato alla sua implementazione la trova nei sorgenti del ThereminoGeiger – cercare tutte le occorrenze di: “DeadTime”)

Linearizzare la risposta con metodi statistici non degrada le prestazioni di risoluzione e sensibilità ed è quindi meglio che agire con la forza bruta sull’hardware (ad esempio incrementare la velocità dell’ADC o usare un sample-hold)

– – – – – – –

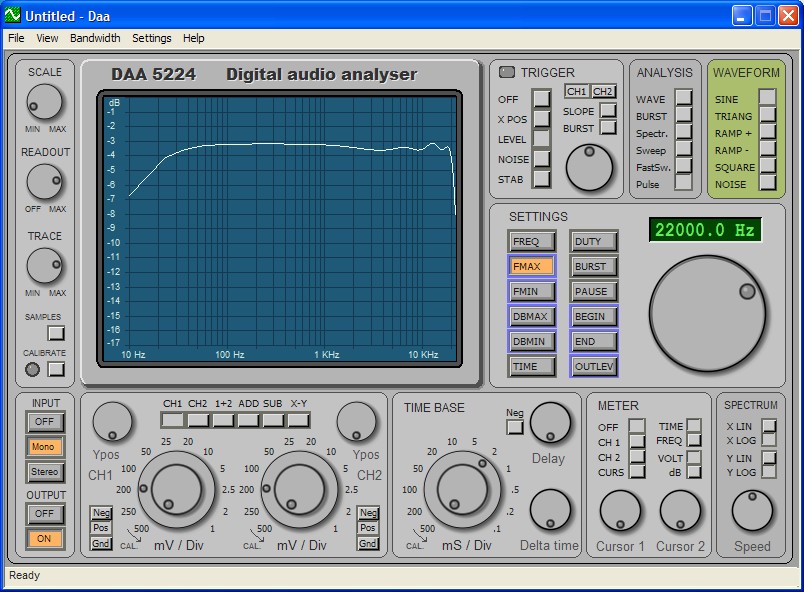
Questi interessanti test hanno portato la nostra attenzione anche sulla banda passante che, in tutte le schede audio è limitata a circa 22 kHz. La frequenza di campionamento minima sarebbe quindi 44 kHz (legge di Nyquist), ma internamente le schede attuano un sovra-campionamento, a volte x2 (e sono quindi definite da 96 kHz) a volte x4 (e sono quindi da 192 kHz). In tutti i casi i dati vengono poi interpolati a 192 kHz, generando impulsi con andamento molto graduale. E questo è esattamente quel che serve, per misurare con esattezza il picco dell’impulso.

Qui si vede la banda passante delle schede audio, che va da 10 Hz a 22 kHz.

Se usassimo un ADC senza la limitazione di banda, dovremmo comunque integrare i dati, fino a ottenere impulsi morbidi, per poterli misurare con precisione.

Senza integrazione, il rumore sarebbe molto alto, a causa della esagerata banda passante. Si perderebbe quindi la possibilità, di vedere gli isotopi di bassa energia e anche la sensibilità e la risoluzione, si ridurrebbero.

– – – – – – –

Concentrarsi molto sulla frequenza di campionamento, a spese di tutto il resto, non è una buona idea. Nel migliore dei casi, si potrebbero aumentare i conteggi massimi di due, tre, o al massimo, dieci volte, ma nella pratica non basterebbe, facciamo degli esempi:

Le reti di rilevamento dei terremoti hanno lo stesso problema, tutti i geofoni in prossimità di eventi catastrofici, saturano e i loro dati vengono semplicemente scartati.

Se anche si usassero sensori in grado di sopportare questi eventi, li si dovrebbe scartare lo stesso, a causa dei forti errori di misura causati dalle discontinuità che si verificano in prossimità dell’epicentro.

Nel caso dei terremoti, le discontinuità sono dovute a fratture del terreno e discontinuità localizzate dovute a rocce e sabbia. Invece nel caso di esplosione di centrali, come Fukushima e Chernobyl, le discontinuità sono dovute alla proiezione di frammenti relativamente grandi, strappati dalle barre del nocciolo.

I frammenti più grandi ricadono in un area di decine di chilometri, rendendo completamente inaffidabili tutti i sensori di quell’area. Se un frammento, come ad esempio quello trovato da Bionerd23 in una aiuola (www.youtube.com/watch?v=ejZyDvtX85Y), cade in prossimità del sensore, questo misurerà valori altissimi, rispetto a tutta la zona circostante.

Si potrebbero avere enormi errori di misura (anche 100 volte), spostandosi di pochi metri. La miscela di isotopi verrebbe completamente alterata, a seconda della composizione del frammento.

– – – – – – – – –

Prendiamo come esempio la rete ambientale tedesca, basata su 1800 sensori Geiger, distanziati mediamente a dieci chilometri uno dall’altro. In caso di evento veramente catastrofico, si dovrebbero scartare quattro o anche dieci sensori, ma i restanti 1790 fornirebbero dati, che estrapolati, permetterebbero di definire esattamente la radioattività all’epicentro.

La legge di attenuazione quadratica, può fornire risultati molto più precisi di quel che potrebbero fare i sensori scartati.

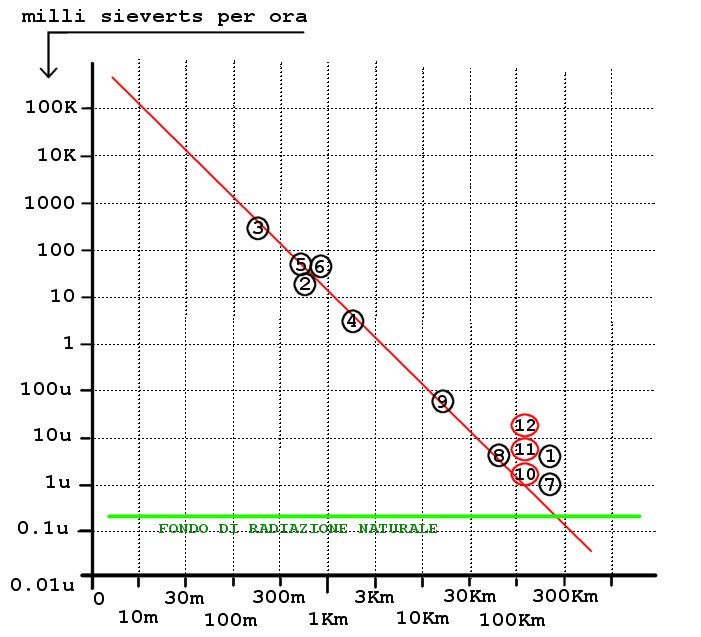
La seguente immagine fa parte di un articolo che abbiamo pubblicato dopo l’incidente di Fukushima, ed è basata sui dati pubblicati nei 15 giorni dopo l’esplosione del reattore 3.

– PDF del documento: Probabilita-e-Rischi

– Decumento ODT per i traduttori: Probabilita-e-Rischi

(1) 15/03/2011 a Tokyo 3 micro-sievert/ora ( 10 volte il fondo di radiazione naturale )
(2) 15/03/2011 “all’ingresso della centrale” 11.9 milli-sievert/ora
(3) 15/03/2011 “nei pressi del reattore tre” 400 milli-sievert/ora
(4) 17/03/2011 misurato dagli elicotteri 4.13 milli-sievert da 1000 piedi di altezza ( 1600m )
(5) 17/03/2011 misurato dagli elicotteri 50 milli-sievert da 400 piedi di altezza ( 640m )
(6) 17/03/2011 misurato dagli elicotteri 87.7 milli-sievert da 300 piedi di altezza ( 480m )
(7) 18/03/2011 a Tokyo misurato un livello delle radiazioni di circa 1 micro-sievert/ora
(8) 18/03/2011 a 60 chilometri dalla centrale 6,7 micro-sievert/ora.
(9) 18/03/2011 a 20 chilometri dalla centrale 80 micro-sievert/ora.
(10) 18/03/2011 a Ibaraky 140 chilometri dalla centrale 2.5 micro-sievert/ora.
(11) 20/03/2011 a Ibaraky 140 chilometri dalla centrale 6.7 micro-sievert/ora.
(12) 21/03/2011 a Ibaraky 140 chilometri dalla centrale 12 micro-sievert/ora.

Dati pubblicati dal “Ministry of Education” (www.mext.go.jp), dalla “Nuclear Safety Division (www.bousai.ne.jp/eng) e dal municipio di Fukushima, dopo i voli in elicottero.

In questa immagine si possono notare tre cose:

• La legge di attenuazione quadratica è perfettamente rispettata. (errori minimi rispetto agli errori dei sensori) 

• I dati sono estrapolabili fino in prossimità dell’evento.

• Si può definire il valore di radioattività fino a pochi metri dall’esplosione con grande precisione.

Con una rete di migliaia di stazioni si potrebbe ottenere un grande precisione, ma nell’intento di non scartare i dati di qualche sensore, si degraderebbe la qualità della intera rete. Piuttosto sarebbe meglio procedere nel senso contrario e cercare di diminuire il rumore e massimizzare la sensibilità e la separazione degli isotopi.

Con i sensori Nai(Tl) la risoluzione è sempre scarsa ed esiste la reale possibilità di misurare un isotopo al posto di un altro. Più la risoluzione diminuisce e maggiore è questo rischio.

Linearizzazione delle energie 

Theremino MCA usa un equalizzatore simile agli equalizzatori grafici per linearizzare le energie e le ampiezze dei grafici.

Molti hanno espresso dubbi sul fatto che questo metodo sia meno preciso di quello dei punti con energia selezionabile (Equalizzatore parametrico) usato, ad esempio, nella versione 6 del PRA.

Pertanto è necessario spiegare il perché di questa scelta.

Linearizzare punti arbitrari, non equamente distribuiti lungo lo spettro, può produrre curve innaturali e grandi errori.

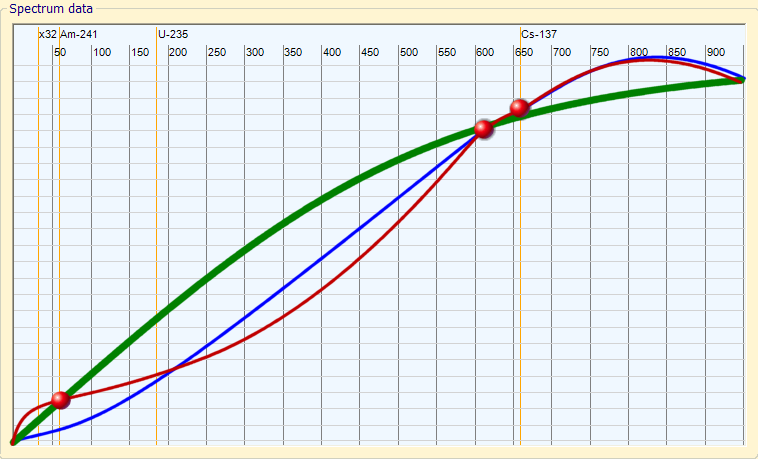
VERDE: La migliore curva di linearizzazione, che minimizza gli errori.
BLU: La curva di linearizzazione che si ottiene correggendo “quasi” esattamente il 609 e il 662 KeV
ROSSO: La curva finale, dopo aver corretto “esattamente” anche il 59 KeV

“Lingua italiana” – Grandi errori prodotti da un sistema di linearizzazione “preciso” —————————————————————————————————————————————————————— 1) L’utente corregge “esattamente” un picco del Cs-137 a 662 keV (con un campione di cesio)

2) L’utente corregge “esattamente” un picco del Bi-214 a 609 KeV (con un campione di radio)

3) A causa della imprecisione introdotta dalla grande FWHM delle righe, e anche perché il numero di bin non è infinito, quelle “esatte” correzioni non sono così “esatte”

4) Poiché la distanza tra i due punti di correzione (609 e 662) è piccola, ogni piccola imprecisione estrapola un grande errore sulla intera curva di correzione.

5) L’utente prova un campione di Am-241 a 59,536 KeV, scopre un grande errore,  e corregge “esattamente” il picco.

6) L’utente prova un campione di Co-60 a 1.3 MeV, scopre un grande errore, e corregge “esattamente” questo errore.

7) L’utente ora è molto felice, tutti i 4 campioni sono “esattamente” corretti  e la sua linearità è assolutamente perfetta …. vero?

No! La curva “invisibile” risultante è più simile ad un serpente che a una curva del mondo reale. Solo i punti a 59, 609, 662 e 1300 KeV sono esattamente corretti, tutte le altre energie sono sbagliate, e con errori maggiori di quelli che si avrebbero senza l’utilizzo di alcuna correzione. Tutte le analisi future fatte da questo “utente felice” rileveranno con “precisione” isotopi che si possono trovare solo su campioni provenienti dal pianeta Marte.

 

“English language” – Great errors produced by a “precise” linearization method —————————————————————————————————————————————————————— 1) The user corrects “exactly” a Cs-137 peak at 662 KeV (using a cesium sample)

2) The user corrects “exactly” a Bi-214 peak at 609 KeV (using a radium sample)

3) Because of the imprecision introduced by the large FWHM of the rows, and because the bin number is not infinite, those “exact” corrections are not so “exact”

4) Since the distance between the two correction points (609 and 662) is little, every little imprecision extrapolates a great error on the entire correction curve.

5) The user tests a Am-241 sample at 59.536 KeV, discovers a great error, and corrects “exactly” the 59 KeV peak

6) The user tests a Co-60 sample at 1.3 MeV, discovers a great error, and corrects “exactly” this error

7) The user now is very happy, all the 4 samples are “exactly” corrected and the linearity is absolutely perfect…. is it true ?

No! The “invisible” resulting curve is more similar to a snake, than to a real world curve. Only the points at 59, 609, 662 and 1300 KeV are exactly corrected, all the other energies are wrong, and with more errors than before of this “linearization” All the future analisys made by this “happy user” will find with “precision” isotopes that can be found only on samples coming from Mars planet.

Overfitting

Su Wikipedia si può leggere un’ottima spiegazione di questo effetto: http://en.wikipedia.org/wiki/Overfitting

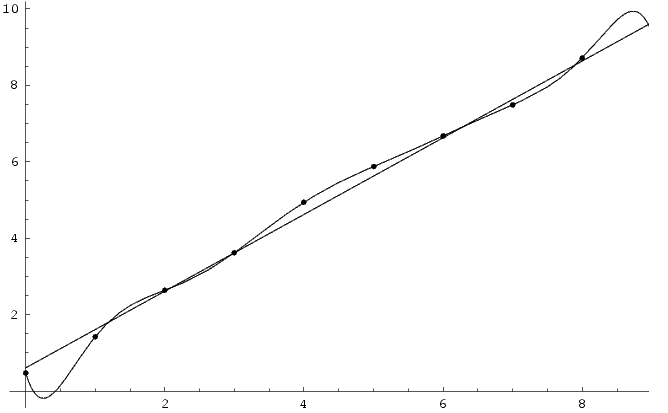
 Wikipedia mostra questa immagine e spiega molto bene che:

ITALIANO: Sebbene la funzione di linearizzazione passi esattamente per tutti i punti si otterrebbe un miglior risultato con una retta.

ENGLISH: Although the polynomial function passes through each data point, the linear version is a better fit.